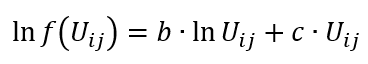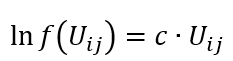Mit der Funktion Gravitationsparameter schätzen (kurz KALIBRI) können zwei verschiedene Nutzenfunktionen für das Gravitationsmodell der Verkehrsverteilung kalibriert (geeicht) werden (Bestimmung der Parameter b und c).
1.
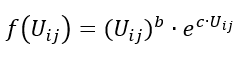
wobei
|
Uij |
Wert für den Nutzen (zum Beispiel abhängig von Entfernung oder Fahrzeit) zwischen Bezirk i und Bezirk j |
|
b,c |
zu schätzende Parameter |
2.
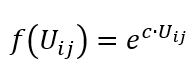
wobei
|
Uij |
Wert für den Nutzen (zum Beispiel abhängig von Entfernung oder Fahrzeit) zwischen Bezirk i und Bezirk j |
|
c2 |
zu schätzender Parameter |
Die Funktion KALIBRI passt diese Nutzenfunktionen an eine vorgegebene Fahrtweitenverteilung an.
Anschließend berechnet die Funktion Verkehrsverteilung mit Hilfe des Gravitationsmodells aus dem bekannten Quellverkehr Qi eines Bezirks i sowie dem bekannten Zielverkehr Zj eines Bezirks j und den hier bestimmten Parametern b, c (oder nur c) den Verkehrsfluss Fij von Bezirk i nach Bezirk j (Gravitationsmodell rechnen).
Die Funktion KALIBRI bietet zwei verschiedene Möglichkeiten, die Parameter für das Gravitationsverfahren zu schätzen:
Die Parameter b, c oder c werden in einem iterativen Prozess bestimmt. Dabei wird die Nutzenfunktion logarithmisch transformiert; es gilt dann:
oder
Innerhalb jeder KALIBRI-Iteration wird eine vorläufige Nachfragematrix (zum Beispiel durch das Multi-Verfahren bei einer zweiseitig gekoppelten Gravitation) bestimmt. Die daraus resultierenden Funktionswerte der Nutzenfunktion werden mit Hilfe einer linearen Regression geglättet, und zwar so lange, bis die maximale Anzahl der KALIBRI-Iterationen erreicht ist oder keine Veränderung der Werte mehr auftritt. Die geglätteten Funktionswerte beschreiben dann eine Funktion des Typs [2] oder [3].
Falls eine Protokolldatei erzeugt wird (Option im Register Ausgaben), können Sie darin eine Zusammenfassung der Schätz-Ergebnisse finden. Dabei wird auch die Güte der Schätzung angegeben. Sie ist definiert durch
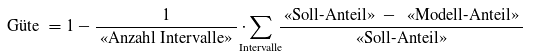
und stellt die durchschnittliche relative Abweichung der Anteile im Modell von den empirisch gemessenen Soll-Anteilen dar. Im Idealfall beträgt die Güte 1 (perfekte Übereinstimmung) und nimmt mit kleiner werdenden Werten ab. Eine negative Güte ist gleichbedeutend mit sehr starken Abweichungen und somit einer eher schlechten Parameterschätzung.